Pearson BTEC Level 5 Higher National Diploma in Electrical and Electronic Engineering/Manufacturing Engineering
| COURSE TITLE | Pearson BTEC Level 5 Higher National Diploma in Electrical and Electronic Engineering/Manufacturing Engineering | ||
| STUDENT NAME | |||
| MODULE TITLE | Unit 5006: Further Engineering Mathematics | ||
| TITLE OF ASSIGNMENT | FM3: Graphical and numerical methods
FM4: Differential equations |
||
| DEADLINE DATE FOR SUBMISSION BY STUDENTS | 05/01/2026 | ||
| ISSUE DATE | 15/09/2025 | ||
| FORMATIVE FEEDBACK DATE | 29/12/2025 | ||
| SUBMISSION LOCATION | Turnitin | ||
| ASSESSOR(S) | Md Akmol Hussain | ||
| IV NAME | Arshad Ahmed Mir | ||
| LEARNING OUTCOMES ASSESSED
LO3: Approximate solutions of contextualised examples with graphical and numerical methods LO4: Review models of engineering systems using ordinary differential equations |
|||
NOTES FOR STUDENTS
What is Academic Malpractice?
Academic malpractice relates to academic work that does not meet normal standards of academic practice and encompasses all kinds of academic dishonesty, whether deliberate or unintentional, which infringes the integrity of the College’s assessment procedures. ‘Candidate malpractice’ means malpractice by a candidate in the course of any examination or assessment, including the preparation and authentication of any controlled assessments or coursework, the presentation of any practical work, the compilation of portfolios of assessment evidence and the writing of any examination paper.
| Learner declaration (authentication) |
| I certify that the work submitted for this assignment is my own and research sources are fully acknowledged.
Student signature: Date: |
Assessment Brief
| Student Name/ID Number | |
| Unit Number and Title | Unit 5006: Further Engineering Mathematics |
| Academic Year | 2025/26 |
| Unit Tutor | Md Akmol Hussain |
| Assignment Title | FM3: Graphical and numerical methods |
| Review date | 22/12/2025 |
| Submission Date | 05/01/2026 |
| IV Name | Arshad Ahmed Mir |
| Submission Format |
| Instruction to students:
● To maximise your learning outcome, attempt all tasks in this assignment. ● Submit your assignment with your signed front sheet (for authentication) to TurnItIn. |
LO3: Approximate solutions of contextualised examples with graphical and numerical methods
Assignment Brief and Guidance
Scenario
You are working as an engineer for a multinational manufacturing organisation who has just taken on some new apprentices. The research and development department has requested your assistance in the design of a booklet containing set worked engineering questions and their associated advanced mathematical techniques. This training booklet will be used aspiring engineers by developing solutions to real world problems. Therefore, solve the following tasks and describing your thought process.
Task 1
In operations research, the solutions to problems can frequently be estimated with graphical methods. In this task you have to maximise the profit (Z). The relationship with two other variables (x, y) as well as their constraints is shown below:
Z = 3x + 10y
Constraints: 2x + 5y16, x0, y 0 and x5.
Task 2
A ball is drifting on the surface of the water (see Figure below). The question investigated here is: If the radius and water density are known, how deep does the ball sink in?

Figure 1: Drifting ball
The approach is centred around the fact that the buoyancy and gravity are in equilibrium and, therefore, the following equation needs to be solved for x, and the roots be determined. Use both the bisection method and the Newton–Raphson method to perform this task (i.e first, find the roots using bisection method, then use newton-raphson method to also find the roots). Conduct the number of iterations required to achieve an error tolerance ∊ ≤ 0.05%.
Where:
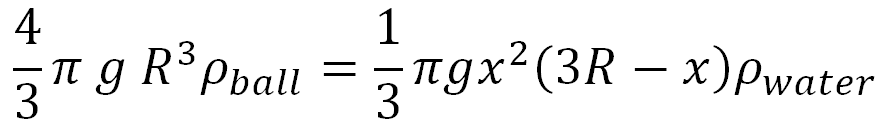
g: Gravitational constant
R: Radius of ball
ρball: Density of ball (500 kg/m3)
ρwater: Density of water (1000 kg/m3)
Task 3
Determine the approximate value of the following integral using two different numerical integral methods.
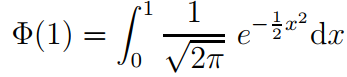
Task 4
The charging of a capacitor through a resistor can be modelled by a first order differential equation. Develop a model for the capacitor voltage (assume no prior charge) for a step input of 5 V (at t =0), a capacitor of 20μF and resistor of 850Ω. Graph the capacitor voltage for the first five time constants.
Write an essay critiquing the use of numerical estimation methods, commenting on their applicability and the accuracy of the methods. (Suggested word count: 500 words, use at least two textbook references)
Learning Outcomes and Assessment Criteria |
|||
| Learning Outcome | Pass | Merit | Distinction |
| LO3 Approximate solutions of contextualised examples with graphical and numerical methods
|
P6 Estimate solutions of sketched functions using a graphical estimation method
P7 Calculate the roots of an equation using two different iterative techniques P8 Determine the numerical integral of engineering functions using two different methods
|
||
